Определение прямой в геометрии, Координатная прямая (числовая прямая), координатный луч

Упорядоченные пары: каждая точка на координатной плоскости называется парой чисел, порядок которых важен; эти числа записываются в круглых скобках и разделяются запятой. Не зная алгоритм сборки, можно вообще не собрать его КР. Этим фактом когда-то воспользовались Лобачевский и Риман и создали целые геометрии с кривыми прямыми.
Кубик Рубика в четвертом измерении. Для начала, что такое взгляд из высшего измерения? Считается, что из высшего измерения можно увидеть полностью фигуры базового измерения. Например, на плоскости мы можем видеть точку- фигуру 0 измерения, прямую- фигуру 1 измерения, прямую в виде точки, двухмерные фигуры- треугольник, круг. В пространстве можно видеть точки, линии, плоскости, пространственные фигуры меньших размеров. В большинстве случаев фигуры непрозрачные и нам, что бы увидеть их внутреннее содержание, нужно разделить, "просветить", "прозвучить" их.
Иногда это невозможно и приходится мысленно рассекать и соединять их. Считается, что фигура базового измерения полностью может быть видна в высших измерениях: точка из линии, линия из плоскости, плоскость из пространства, 3-х мерное пространство из 4 измерения. Вот последним сейчас и займемся. Перед нами известная головоломка- Кубик Рубика КР , представляющая собой устройство, состоящее из большого куба, разделенного на малые кубики с возможностью закрепления и перемещения их.
Первоначальное значение кубиков 3х3х3, его и рассмотрим. КР состоит из видимых 26 малых кубиков, 27 невидимый, 6 граней, состоящих из 9 кубиков, всего 54 поверхности, окраска граней- верхняя- желтый цвет, нижняя, невидимая- белый, левая- красный , правая невидимая, противоположная красной- оранжевый, правая- зеленый, левая невидимая, противоположная зеленой- синий.
В динамике при поворотах центральные кубики граней остаются на месте. Число сочетаний кубиков- 43 , число перестановок- Игрок, зрительно воспринимая КР, одновременно видит из 1 точки глаза наблюдателя 1,2 или 3 грани КР. Центральный кубик остается невидимый.
Перед игроком стоят 2 задачи- "разобрать" грани КР из первоначального состояния в вероятностное и собрать его до первоначального. Не зная алгоритм сборки, можно вообще не собрать его КР. Наша задача- увидеть все кубики, снаружи и изнутри, включая их раскраску. Усложним задачу- представим, что все 27 кубиков окрашены в цвета КР.
Для этого мысленно рассечем КР из 6 осевых точек методом совмещения осей координат игровая геометрия. На игровом пространстве трехмерной настольной игры "Ставропольские шары" ИП ТНИ СШ , на 1 секторе на центральных ячейках расположим ячейки, окрашенные в желтый цвет 9шт , на 2,3,4 секторах слева от центральных ячеек- ячейки красного цвета всего 9 шт , справа- оранжевого 9 , сверху- синего 9 и снизу- зеленого 9 , в центре ИП, в 3 секторе будет находиться еще желтая ячейка невидимый центральный кубик , на 5 секторе- в центре ячейки белого цвета 9шт.
Это вид спереди. Следующий вид- сзади: 1 сектор белый цвет, 2,3,4 сектора- слева-оранжевый, справа- красный, сверху- зеленый, снизу- синий, в центре 3 сектора- белый цвет, 5 сектор- желтый. Вид слева- 1 сектор красный, 2,3,4 сектора- слева- желтый, справа- белый, сверху- синий, снизу- зеленый, в центре красный цвет, 5 сектор- оранжевый. Вид справа- 1 сектор- оранжевый цвет, 2,3,4 сектора- слева- белый, справа- желтый, сверху- зеленый, снизу- синий, в центре 3 сектора- оранжевый, 5 сектор- красный цвет.
Вид сверху- 1 сектор- синий цвет, 2,3. Вид снизу- 1 сектор- зеленый цвет, 2,3,4 сектора- слева- красный. Это исходное статическое положение , далее можно наблюдать перемещения кубиков и граней его по 6 ИП это модель 4-х мерного куба. Задача- полностью увидеть внешнюю и внутреннюю часть трехмерной фигуры из воображаемого 4 измерения решена с помощью игровой геометрии.
Добрых Вам намерений, светлых мыслей и славных дел. До свидания. Логово Отшельника. Сложно о простом. Прямая и не прямая. Недавно вернулся из Казани, где неоднократно проходил улицу Лобачевского. Естественно задумался о геометриях и почему все настолько простое настолько сложно. Вот например прямая, все знают что такое прямая, многие даже график построить могут. Многие даже узнают уравнение прямой с первого взгляда. Однако дать определение прямой задачка не тривиальная.
Этим фактом когда-то воспользовались Лобачевский и Риман и создали целые геометрии с кривыми прямыми. В смысле любой нормальный человек сразу поймет что у Лобачевского прямой названа гипербола, а у Римана участок окружности и Урок 1. Луч: теория. Параллельность прямых - применение.
Теорема о сумме углов треугольника. Математика - это легко!
Часто встречающиеся понятия. Другое Измерение. Или, опять скажете, это эйнштейнианский вопрос? Если эйнштейнианский, то и понятие будет соответствующим - набором этаких "шариков", раскиданных в пространстве. Эти "шарики" даже можно, как молекулы, склеить в некую полимерную резинотехническую поверхность, которая способна изгибаться. Эйнштейнианцы априори "шариковеды". С топологией никакие переносчики взаимодействия не нужны. Эти "кони" становятся необходимы лишь там, где её нет в эйнштейнианском "шариковом" мире.
Вот и вопрос обоснования полей они строят на "шариках". Для поля массы им нужен пресловутый бозон Хиггса, для гравитации - гравитон, для магнитного взаимодействия - магнон, и т. На самом деле, ПОЛЕ возникает на границе определённых пространств, как проективно двойственное понятие материальной структуры. Согласно этому принципу, точка и прямая ТАМ не различимы они друг другу двойственны. Любая структура Материи, поэтому, способна пребывать в своём двойственном состоянии, и как, собственно, частица, и как волна ПОЛЕ.
ПОЛЕ не состоит ни из каких "шариков" "состоять из" - прерогатива лишь нашего вещественного мира. Почему в эйнштейнианской концепции ничего этого нет? Потому, что у них нет различения пространств в их подвижности и взаимотрансформации. Все эфирные концепции пьют из этого же тухлого источника.
И была последняя горше первой. Занятие 1. Положение точки в пространстве. Плоскости проекций. Чертежи геометрических объектов в задачах по начертательной геометрии выполняют в двух или трех проекциях. Плоскость проекций — двухмерна, а пространство — трехмерно. Невозможно на одной плоскости точно изобразить вид какой-либо объемной детали со всех сторон — спереди, сверху, сбоку.
Поэтому эти виды изображают в трех ракурсах, которые называют проекциями. Самый простой геометрический объект - это точка. Точку никак нельзя измерить — у нее нет ни длины, ни ширины, ни высоты, ни площади, ни объема Принцип Кавальери. ОГЭ математика. Прямоугольник, ромб, квадрат. Мама, ты космос! Геометрические понятия: плоскость, точка, прямая, отрезок, луч, угол. Математическая продлёнка.
Самый правильный угол. Что такое прямой угол? Почему дома, вагоны, книжки и коробки преимущественно прямоугольные? Почему расстояние от точки до прямой вычисляется вдоль перпендикуляра?
Как построить прямой угол без циркуля и линейки? Что такое вертикаль и горизонталь и почему с горизонтального стола ничего не скатывается? Почему декартовы координатные оси располагаются под прямым углом? Почему ортогональные геометрические векторы перпендикулярны? Как работает теорема Пифагора в неевклидовых геометриях? Мы найдём ответы на все приведённые выше вопросы, используя одно единственное свойство прямого угла.
Нахождение натуральной величины отрезка прямой урок 6. Как вы, вероятно, уже догадались, отрезок прямой общего положения не проецируется в натуральную величину ни на одну из плоскостей проекций, поэтому выполняют некоторые преобразования чертежа.
Существует несколько способов нахождения натуральной величины: В этом уроке рассмотрим первые два. Метод прямоугольного треугольника Итак, в чем же заключается метод прямоугольного треугольника? Сущность метода заключается в нахождении гипотенузы прямоугольного треугольника.
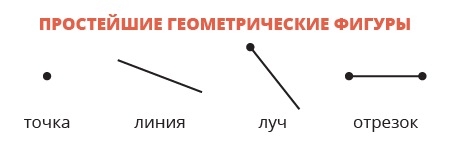
В прямоугольном треугольник должен Цивилизация Хамилия. Сколько измерений в Абсолюте. Всякая более сложная геометрическая фигура — это множество точек, обладающих определенным свойством, характерным только для этой фигуры. Прямую можно представить себе как бесчисленное множество точек, которые расположены на одной линии, не имеющей ни начала, ни конца. На листе бумаги мы видим только часть прямой линии, так как она бесконечна.
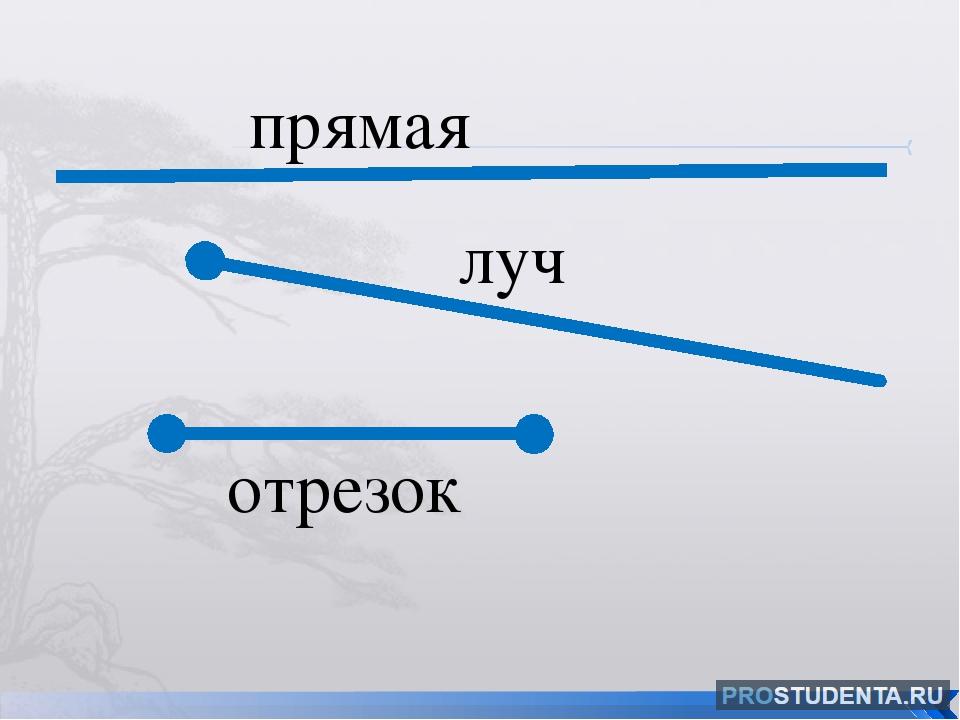
Прямая изображается так:. Часть прямой линии, ограниченная с двух сторон точками, называется отрезком или отрезком прямой. Основное свойство отрезка — это его длина.
Длина отрезка — это расстояние между его концами. Измерить отрезок — это значит установить его длину в определенных единицах. Основные единицы измерения длины: миллиметр мм , сантиметр см , дециметр дм , метр м , километр км. Луч — это направленная полу прямая, которая имеет точку начала и не имеет конца.
Луч изображается так:. Если на прямой вы поставили точку, то этой точкой прямая разбивается на два противоположно направленных луча. Такие лучи называются дополнительными.

Плоскость , как и прямая, — это первичное понятие, не имеющее определения. У плоскости, как и у прямой, невозможно увидеть ни начала, ни конца. Мы рассматриваем только часть плоскости, которая ограничена замкнутой ломаной линией. Примером плоскости является поверхность вашего рабочего стола, тетрадный лист, любая гладкая поверхность. Плоскость можно изобразить как заштрихованную геометрическую фигуру:.
Взаимное расположение прямой и точки. Возможны два варианта взаимного расположения прямой и точки на плоскости:. Аксиома — это утверждение, устанавливающее некоторое свойство и принимаемое без доказательства. Основные свойства взаимного расположения точек на прямой и на плоскости. Правильность утверждения о свойстве той или иной геометрической фигуры устанавливается путем рассуждения. Это рассуждение называется доказательством. А само утверждение, которое доказывается, называется теоремой.
Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы.

В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Обратите внимание! В AlmaU , Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Право, всемирная история, биология, химия и творческий экзамен.